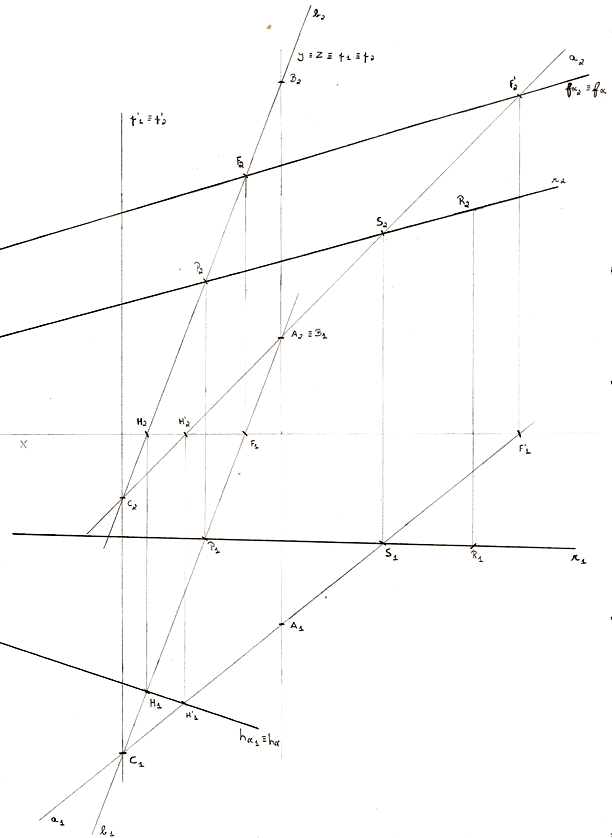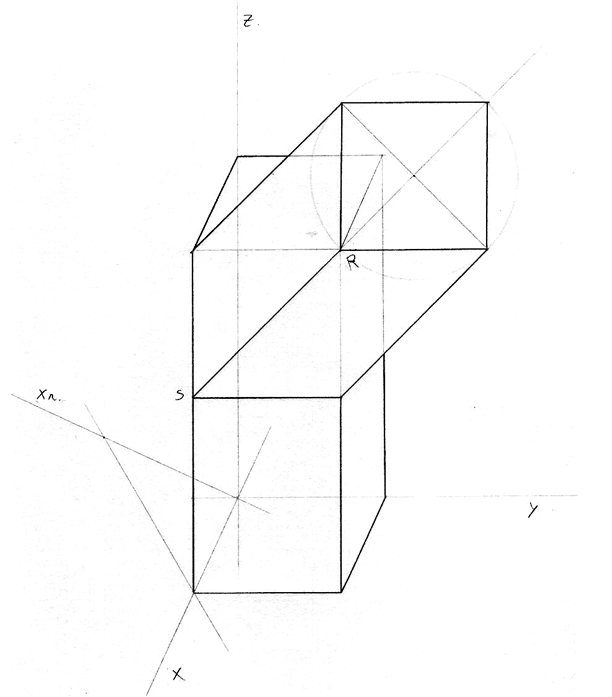Exercícios resolvidos por alunos - 10º e 11º anos
Exercícios resolvidos por alunos de várias escolas do país, entre os anos de 2006 e 2014. Os exercícios foram apresentados como desafios, pelo que alguns apresentam um grau de dificuldade elevado, considerando que são dirigidos aos alunos do ensino secundário.
Enunciados de Elísio Silva.
Plano (1-8)
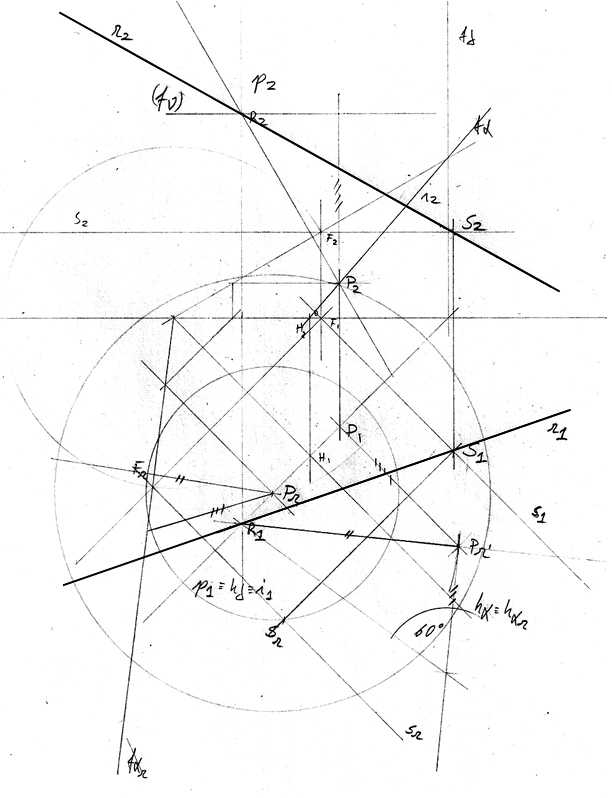
Exercício 1
Representa os traços, nos planos de projeção, dos planos α e θ.
Dados
- o plano α contém a reta p, de perfil, e o plano θ contém a reta p', também de perfil;
- a reta p é passante e passa pelo ponto P (-4; -6; -3);
- a reta p' tem a mesma abcissa da reta p e o seu traço frontal tem cota positiva;
- as retas p e p' são paralelas e distam 5 cm entre si;
- o ponto C (5; 7; 3) é comum aos dois planos
Proposta de resolução
Exercício 2
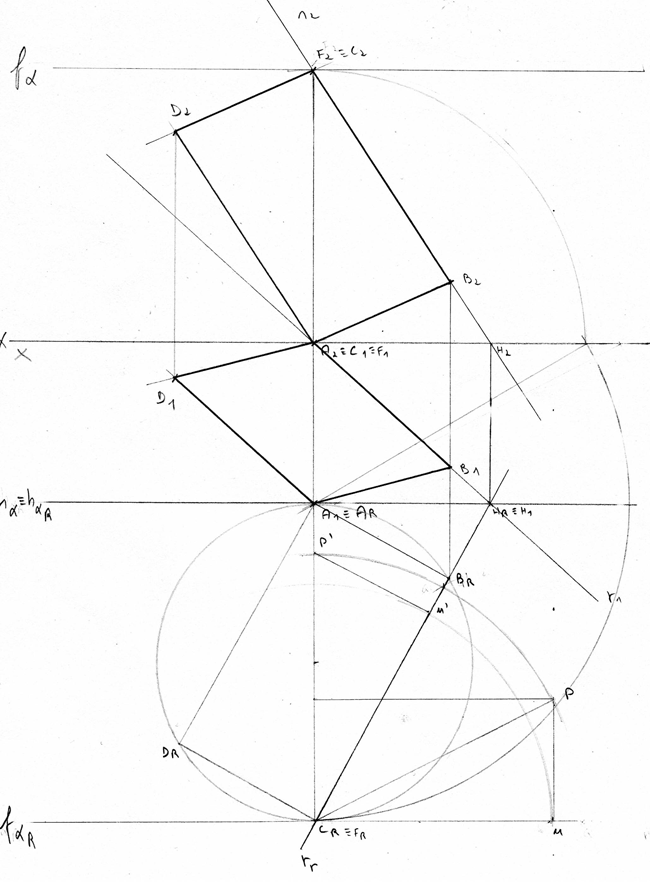
Considera o plano α definidas pelas retas p e p’, paralelas.
Representa os traços do plano α nos planos de projeção.
Representa, ainda, as projeções da reta r pertencente ao plano α.
Dados
- a reta p é de perfil e está definida pelos pontos A (0; 6;3) e B (-3; 11);
- a reta p’ contém o ponto C (5; 10; -2);
- a reta r contém o ponto R, com -6 cm de abcissa e 7 cm de cota, e sua projeção frontal faz um ângulo de 15° (a.d.) com o eixo x.
Proposta de resolução
Exercício 3
Representa em dupla projeção ortogonal, sem recorrer a processos geométricos auxiliares, os traços nos planos de projeção do plano α.
Dados
- o plano está definido pelo ponto A (7; 7; -3) e pela reta p;
- a reta p é de perfil passante e contém o ponto P(0; 8; 4).
Proposta de resolução
Exercício 4
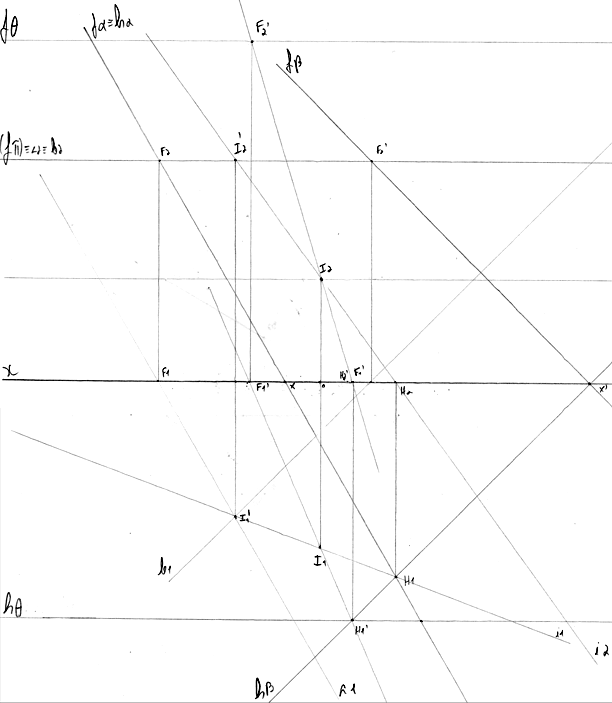
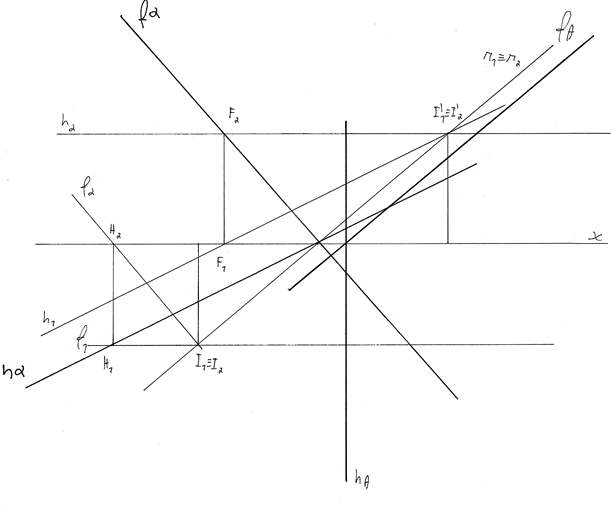
Representa os traços nos planos de projeção dos planos θ e α.
Dados
- os pontos A e C pertencem a ambos os planos, B pertence ao plano α e D ao plano θ;
- o traço frontal do plano α faz um ângulo de 45° (a.d.) com o eixo x e o traço horizontal do plano θ faz , também com este eixo, um ângulo de 60° (a.e.);
- A tem – 7 cm de abcissa e 3 cm de cota;
- B tem 4 cm de abcissa e pertence a ambos os planos de projeção;
- C tem – 7 cm de abcissa e 2 cm de cota;
- D (-2; 3; 2).
Proposta de resolução
Exercício 5
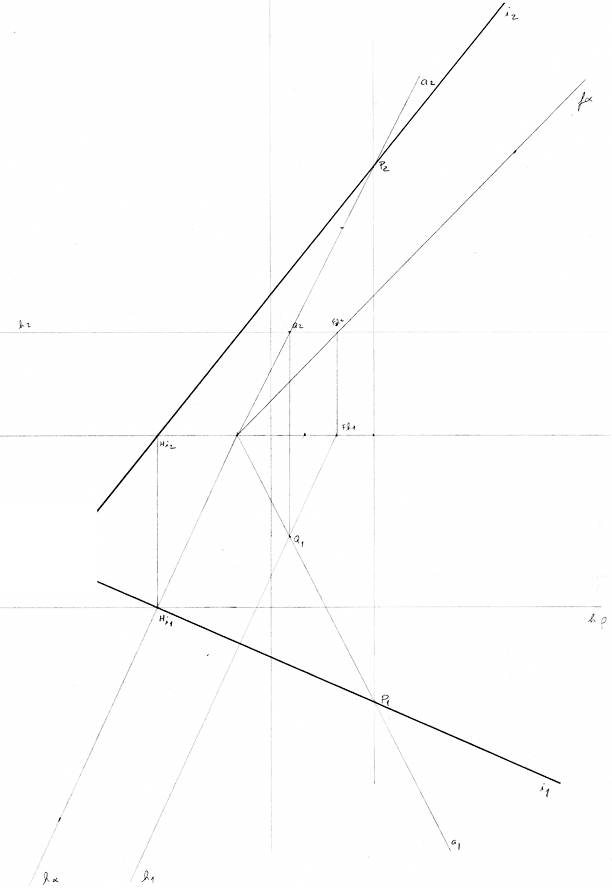
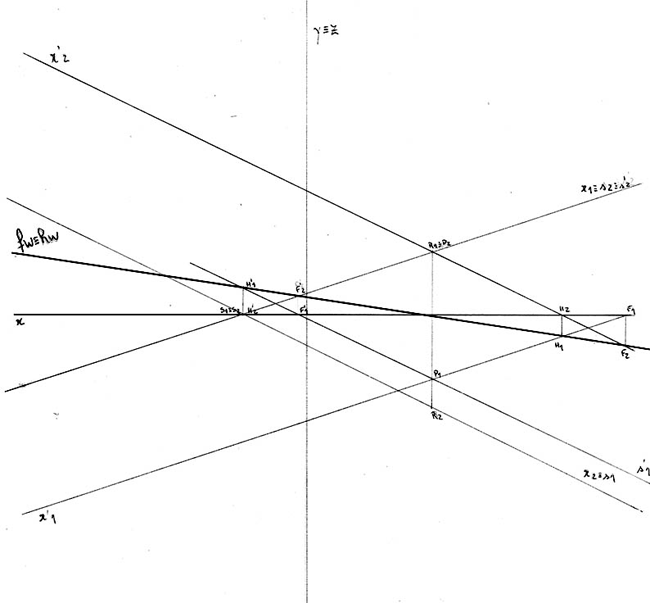
Representa os traços, nos planos de projeção, dos planos α e α’.
Dados
- As retas de maior inclinação i e i’, respetivamente dos planos α e α’, são concorrentes no ponto H (6; 6; 0);
- os traços horizontais dos planos são coincidentes e intersetam o eixo x num ponto com -5 cm de abcissa;
- o traço frontal da reta i tem 4 cm de cota e abcissa positiva;
- o traço frontal da reta i´ tem 5 cm de cota e abcissa negativa.
Proposta de resolução
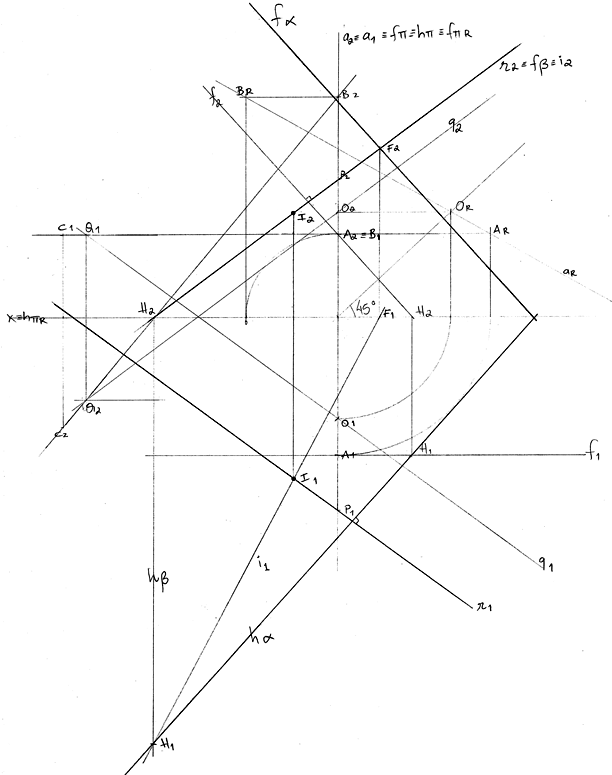
Exercício 6
Representa as projeções do ponto P, sabendo que tem 6 cm de cota e pertence aos planos α e θ.
Dados
- o plano θ é de rampa e os seus traços têm 4 cm de cota e -4 cm de afastamento, respetivamente os traços frontal e horizontal;
- o traço frontal do plano α faz um ângulo de 60° (a.e.) com o eixo x e coincide com o traço horizontal deste plano;
- o plano α contém o ponto de coordenadas nulas.
Proposta de resolução
Exercício 7
Representa os traços nos planos de projeção do pano α, sabendo que este plano está definido por duas retas concorrentes, p e r.
Dados
- o ponto de concorrência pertence ao plano horizontal de projeção;
- a reta p é de perfil, tem -4 cm de abcissa e está contida no β13;
- as projeções da reta r fazem ângulos de 50º (a.e.) e de 20º (a.d.) com o eixo x, respetivamente a projeção frontal e a projeção horizontal.
Proposta de resolução
Exercício 8
Determine as projeções de uma reta n de nível (horizontal) com 2 cm de cota e concorrente com as retas de perfil p e p’, sem recorrer a processos geométricos auxiliares (rebatimentos; rotações; mudança do diedro de projeção).
Dados
- a reta p contém os pontos R (0; 0; 0) e S (7; 8);
- a reta p’ contém os pontos M (-4; 6; 1) e N (-2; 7).
Proposta de resolução
Interseções (9-12)
Exercício 9
Representa as projeções da reta i de interseção dos planos α e ρ.
Dados
- o plano α interseta o eixo x num ponto com 1 cm de abcissa e os seus traços, nos planos de projeção, fazem ângulos de 65° (a.e.) e de 45° (a.d.) com o eixo x, respetivamente o traço horizontal e o traço frontal;
- o traço horizontal do plano ρ é fronto-horizontal e tem 5 cm de afastamento;
- a reta i contém o ponto P;
- o ponto P tem -3 cm de abcissa e pertence ao bissetor dos diedros ímpares.
Proposta de resolução
Exercício 10
Representa as projeções da reta i de interseção dos planos α e θ.
Dados
- o traço horizontal do plano α faz um ângulo de 60° (a.d.) com o eixo x e o traço frontal do plano θ faz, também com este eixo, um ângulo de 60° (a.e.);
- o plano α contêm o ponto F (7; 0; -3) e o plano θ contém o H (-4; 3; 0);
- as projeções da reta i fazem ângulos de 60° (a.d.) e de 60° (a.e.) com o eixo x, respetivamente a projeção frontal e a projeção horizontal.
Proposta de resolução
Exercício 11
Representa o lugar geométrico de intersecção de três planos - α, β, e θ.
Dados
- o plano α é ortogonal ao β24, intersecta o eixo x num ponto com 1 cm de abcissa e o seu traço frontal faz um ângulo de 60º (a.e.) com o eixo x;
- o plano β e ortogonal ao β13, intersecta o eixo x num ponto com -8 cm de abcissa e o seu traço horizontal faz um ângulo de 45º (a.e.) com o eixo x;
- o plano θ é de rampa e o seu traço horizontal tem 7 cm de afastamento;
- o lugar geométrico de intersecção dos três planos tem 3 cm de cota.
Proposta de resolução
Exercício 12
Representa as projeções do ponto I de interseção da reta r com o plano α.
Dados
- a reta r é paralela aos planos θ e β13 e contém o ponto P (-3; 7; 5);
- o plano θ está definido por três pontos: A (-3; 5; 3), B (-3; -3; 8) e C (6; -3; -4);
- o plano α é ortogonal à reta r e contém o ponto A.
Proposta de resolução
Figuras planas (13-15)
Exercício 13
Representa as projeções do retângulo [RSTU] pertencente ao plano vertical α.
Dados
- o plano α interseta o eixo x num ponto -3 cm de abcissa e faz um diedro de 60° (a.d.) com o plano frontal de projeção;
- o vértice R tem 8 cm de cota e pertence ao plano bissetor dos diedros ímpares;
- o vértice T tem 2 cm de cota e também pertence ao plano bissetor dos diedros ímpares;
- o vértice S é o de menor afastamento;
- os lados maiores têm o dobro do comprimento dos lados menores.
Proposta de resolução
Exercício 14
Representa as projeções de um retângulo [ABCD] contido num plano projetante horizontal
Dados
- a diagonal [AC] é paralela ao plano horizontal de projeção e dista deste 3 cm;
- um dos vértices do retângulo pertence ao plano horizontal de projeção e tem afastamento superior ao centro deste polígono;
- A tem -2 cm de abcissa e um cm de afastamento, C tem -6 cm de abcissa e 8 cm de afastamento.
Proposta de resolução
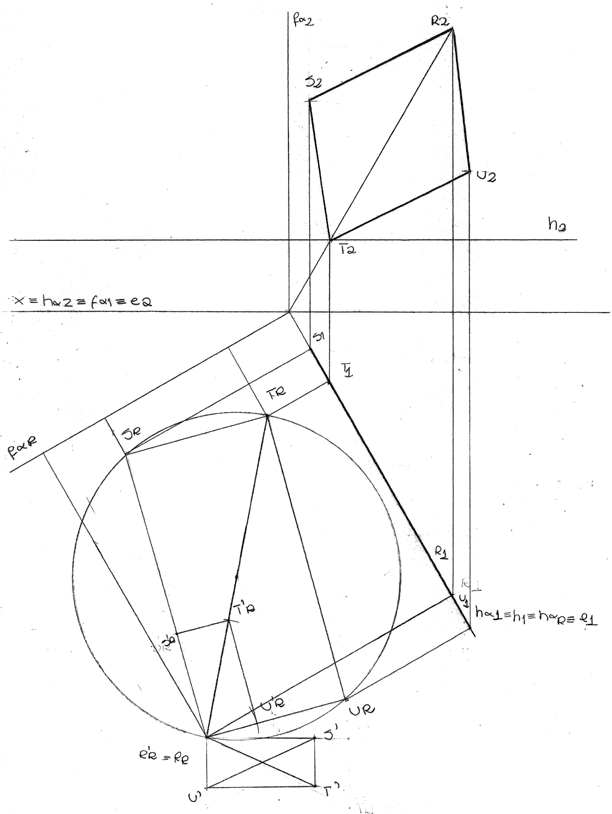
Exercício 15
Determina as projeções de um retângulo [ABCD] contido num plano de rampa.
Dados
- o traço horizontal do plano tem 4 cm de afastamento;
- a diagonal [AC] é de perfil, mede 8 cm e os vértices A e C pertencem aos planos de projeção, respetivamente, plano horizontal e plano frontal;
- B é o vértice mais à direita e tem menor cota do que o vértice D;
- os lados maiores são duplos dos lados menores.
Proposta de resolução
Sólidos (16-21)
Exercício 16
Representa uma pirâmide hexagonal regular de base oblíqua e situada no 1º diedro.
Dados
- o vértice principal da pirâmide tem -3 cm de abcissa e 2 cm de afastamento;
- duas arestas laterais, consecutivas, estão contidas no plano horizontal de projeção e fazem ângulos de 30° e 60° (ambos de abertura à esquerda) com o eixo x;
- os lados da base medem 3 cm.
Proposta de resolução
Exercício 17
Representa, em dupla projeção ortogonal, as projeções de uma pirâmide triangular oblíqua de base regular.
Dados
- a base está contida num plano que faz ângulos iguais com os três planos de projeção (xy, xz e yz);
- a circunferência circunscrita à base tem 3,5 cm de raio, o seu centro tem 4 cm de abcissa e este dista o mesmo em relação aos três planos de projeção (xy, xz e yz);
- cada uma das arestas da base é ortogonal um dos eixos (x, y e z);
- a base é visível nas três projeções;
- V (0; 1; 0).
Proposta de resolução
Exercício 18
Representa as projeções de uma pirâmide triangular regular.
Dados
- a base está contida num plano oblíquo ortogonal ao β13;
- este plano interseta o eixo x num ponto com 4 cm de abcissa e o seu traço horizontal faz um ângulo de 45º (a.d.) com este eixo;
- um dos vértices da base, o de maior cota, pertence ao plano frontal de projeção;
- as arestas laterais formam ângulos de 70º com o plano da base;
- V (4; 7; 8) é o vértice principal da pirâmide
Proposta de resolução
Exercício 19
Representa o contorno aparente de uma esfera, em ambas as projeções (projeção horizontal e projeção frontal).
Dados
- a superfície esférica está definida por 4 pontos: A (2; 4; 3), B (-1; 3; 3), C (-3; 7; 3) e D (1; 8; 8).
Proposta de resolução
Exercício 20
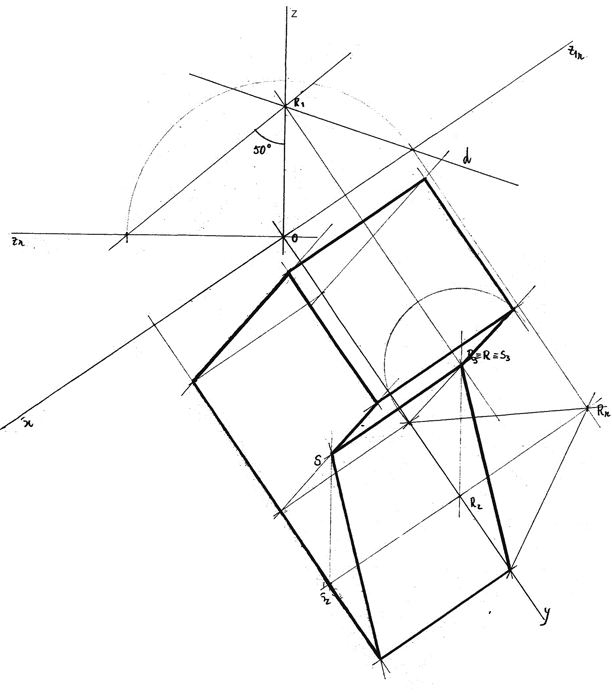
Representa as projeções de um cubo, situado no 1º diedro.
Dados
- [AC] é uma diagonal de uma das faces do cubo;
- A (4; 3; 2), C pertence ao plano frontal de projeção;
- uma das diagonais internas (espaciais) do cubo [AG] é vertical;
- o cubo tem 4 arestas de perfil.
Proposta de resolução
Exercício 21
Representa as projeções de uma pirâmide pentagonal regular
Dados
- a base está contida no plano oblíquo α;
- o plano α interseta o eixo x num ponto com 4 cm de abcissa e os seus traços, nos planos de projeção, fazem ângulos de 45º (a.d.) e de 60º (a.d.), respetivamente, o traço frontal e o traço horizontal;
- o lado de maior cota do pentágono é horizontal e o vértice que lhe é oposto pertence ao plano horizontal de projeção;
- o vértice principal da pirâmide tem -4 cm de abcissa e pertence ao plano horizontal de projeção;
- a pirâmide tem 4 cm de altura.
Proposta de resolução
Paralelismo (22-28)
Exercício 22
Representa os traços nos planos de projeção de três planos - α, α' e α'' - paralelos e equidistantes entre si.
Dados
- os traços frontais dos planos formam ângulos de 60° (a.e.) com eixo x e os seus traços horizontais formam ângulos inferiores a 45°(a.d.), também com o eixo x;
- cada plano contém um ponto: R (-1; 0; 6), S (-6; 5;6) e T (-2; 4; 2), respetivamente os planos α, α'e α''
Proposta de resolução
Exercício 23
Determina os traços dos planos α e β, paralelos entre si.
Dados
- o plano α contém a reta p definida pelos pontos A (0; -7; 7) e B (0; 6; -2);
- o plano β contém os pontos R (0; 2; -2) e S (-5; -3; 3).
Proposta de resolução
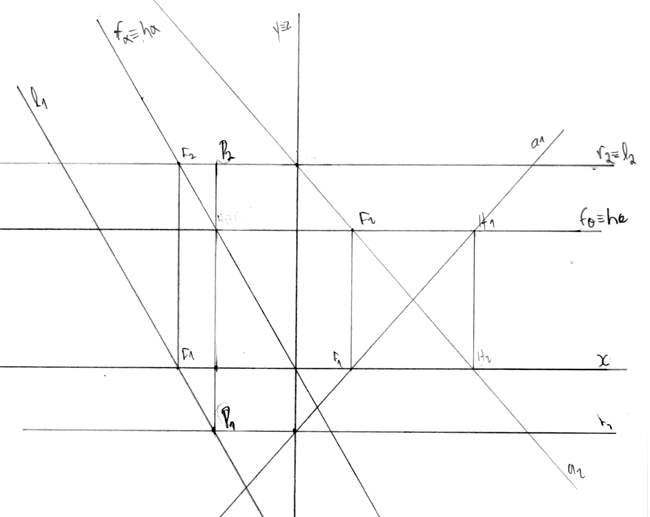
Exercício 24
Determina as projeções da reta r, paralela ao plano α.
Dados
- o plano α está definida por uma das suas retas de maior inclinação - reta i;
- a reta i está contida no β24, interseta o eixo x num ponto com 4 cm de abcissa e a sua projeção frontal faz um ângulo de 50º com o eixo x (a.e.);
- a reta r é paralela ao β13 e contém o ponto R (-2; 5; 4).
Proposta de resolução
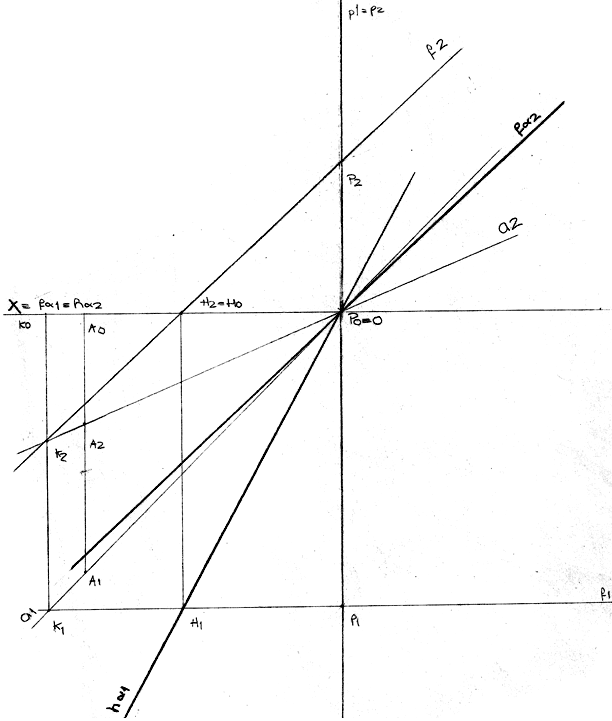
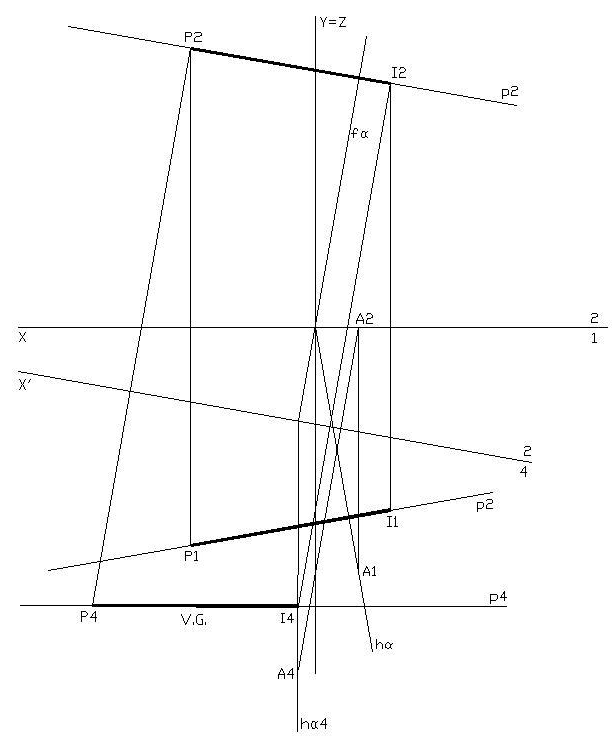
Exercício 25
Determina os traços do plano de rampa θ paralelo à reta de perfil p, sem recorrer a processos geométricos auxiliares (rebatimentos; rotações; mudança do diedro de projeção).
Dados
- o plano θ contém o ponto P (-4; 3; 4);
- a reta de perfil p está definida pelos pontos A (2; -2; 1) e B (3; 3).
Proposta de resolução
Exercício 26
Determina as projeções da reta r, paralela ao plano ω.
Dados
- o plano ω cruza o eixo num ponto com 3 cm de abcissa está definido pelos seus traços;
- os traços fazem com o eixo x ângulos de 45º (a.d.) e de 70º (a.d.), respetivamente, o traço frontal e o traço horizontal;
- a reta r é concorrente com o eixo num ponto com -3 cm de abcissa e a sua projeção horizontal faz um ângulo de 45º (a.d.).
Proposta de resolução
Exercício 27
Determina os traços do plano ω paralelo ao plano θ.
Dados
- o plano θ está definido pelas retas r e s;
- a reta r contém os pontos R (-4; -2; -3); S(2; 0; 0);
- as projeções da reta s são coincidentes com as projeções contrárias da reta r;
- o plano ω contém o ponto P (-4; 2; 2).
Proposta de resolução
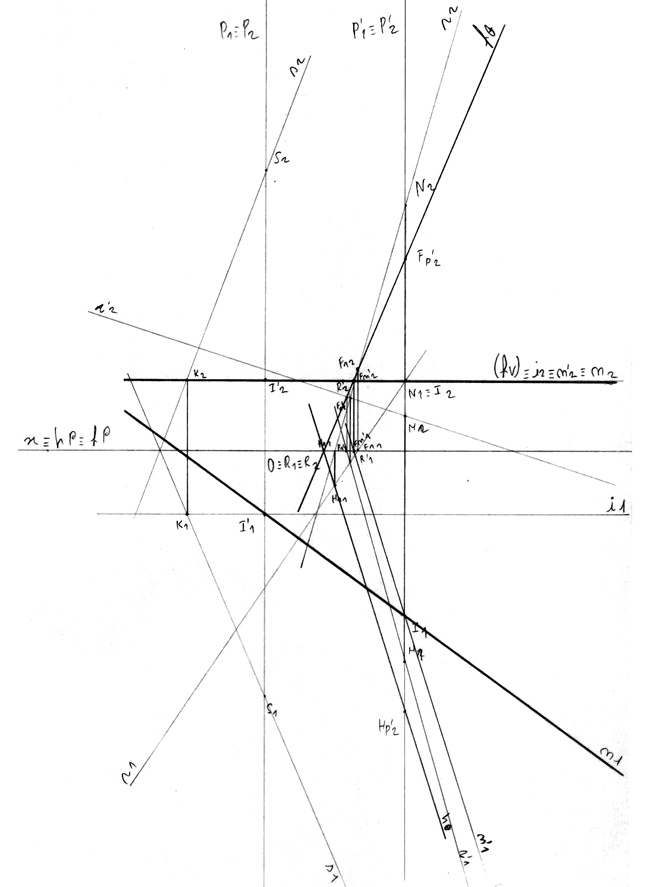
Exercício 28
Dados
- Considera os planos ω oblíquo e θ de topo. Determina os traços do plano α paralelo à reta i de interseção dos planos ω e θ.
- o plano ω interseta o eixo x num ponto com 6 cm de abcissa;
- os traços do plano ω fazem ângulos de 45º (a.d.) e de 60º (a.d.) com o eixo x, respetivamente, o traço frontal e o traço horizontal;
- o plano θ interseta o eixo x num ponto com -8 cm de abcissa e faz um diedro de 30º (a.e.) com o plano horizontal de projeção;
- o plano α contém o ponto P (-2; 0; 2) e o seu traço frontal faz um ângulo de 50º (a.d.) com o eixo x.
Proposta de resolução
Perpendicularidade (29-35)
Exercício 29
Representa os traços, nos planos de projeção, do plano α perpendicular aos planos β e θ sem recorrer a processos geométricos auxiliares (terceira projeção, rotações/rebatimentos e mudança do diedro de projeção).
Dados
- o plano α interseta o eixo x num ponto com 2 cm de abcissa;
- o plano β é passante e contém o ponto P (-5; 5; 3);
- o plano θ está definido pelos pontos A (8; -2; 6), B (-9; 4; -3) e C (8; -3; 4)
Proposta de resolução
Exercício 30
Representa os traços nos planos de projeção dos planos θ e α, sabendo que são perpendiculares entre si.
Dados
- o traço frontal do plano θ interseta o eixo x num com 5 cm de abcissa e faz com este eixo um ângulo de 40º (a.d.)
- o plano α contém a reta r. Esta reta está contida no β24, a sua projeção horizontal faz um ângulo de 40º (a.e.) e interseta o eixo x num ponto com 6 cm de abcissa;
- o plano θ é paralelo à reta r.
Proposta de resolução
Exercício 31
Determina as projeções das retas r, s e t, concorrentes entre si no ponto P.
Dados
- a reta r passa pelo ponto R (2; 2; 2);
- a reta s passa pelo ponto S (-4; 7; 2);
- a reta t passa pelo ponto T (-4; 0: 4);
- as retas são perpendiculares entre si;
- o ponto P tem maior cota do que os pontos R e S
Proposta de resolução
Exercício 32
Determina os traços nos planos de projeção do plano θ ortogonal à reta r.
Dados
- os traços da reta r nos planos de projeção têm 2 cm de abcissa e -2 cm de abcissa, o traço horizontal e o traço frontal respetivamente;
- as projeções da reta r fazem ângulos de 80º (a.d.) e de 70º (a.e.) com o eixo, a projeção frontal e a projeção horizontal respetivamente.
- o plano θ contém o ponto P (2; 7; 5).
Proposta de resolução
Exercício 33
Determina os traços nos planos de projeção do plano θ ortogonal à reta r.
Dados
- os traços da reta r nos planos de projeção têm 2 cm de abcissa e -2 cm de abcissa, o traço horizontal e o traço frontal respetivamente;
- a reta r é paralela ao β24 e a sua projeção horizontal faz um ângulo de 80º (a.e.) com o eixo;
- o plano θ contém o ponto A (0; 7; 5).
Proposta de resolução
Exercício 34
Determina os traços nos planos de projeção do plano ω ortogonal aos planos θ e β13.
Dados
- o plano θ interseta o eixo x num ponto com abcissa nula e os seus traços fazem com este eixo ângulos de 80º (a.e.) e de 45º (a.d.), respetivamente, o traço frontal e o traço horizontal;
- o plano ω interseta o eixo x num ponto com 4 cm de abcissa
Proposta de resolução
Exercício 35
Considera o plano θ ortogonal ao β13. Determina os traços do plano α ortogonal ao plano θ.
Dados
- os pontos A (4; 4; 3) e B (-1; 1; -5) definem a reta r que pertence ao plano θ;
- os planos θ e α intersetam o eixo x no mesmo ponto;
- o traço horizontal do plano α faz um ângulo de 45º (a.e) com o eixo x.
Proposta de resolução
Problemas métricos - Distâncias (36-40)
Exercício 36
Representa a reta r sabendo que esta dista 6 cm do ponto P (-5; 5; 6).
Dados
- a projeção horizontal da reta r interseta o eixo x num ponto com -2 cm de abcissa e faz com este eixo um ângulo de 55° (a.e.);
- o traço horizontal da reta r tem 7 cm de afastamento;
- o traço frontal da reta r tem cota inferior à do ponto P.
Proposta de resolução
Exercício 37
Determina, em dupla projeção ortogonal, as projeções do ponto P, sabendo que este dista 5 cm dos pontos A e B.
Represente, também, as projeções dos segmentos de reta [AP] e [BP].
Dados
- A (4; 3; 5); B (-2; 2; 2);
- o ponto P situa-se no 1º diedro e tem 3 cm de cota
Proposta de resolução
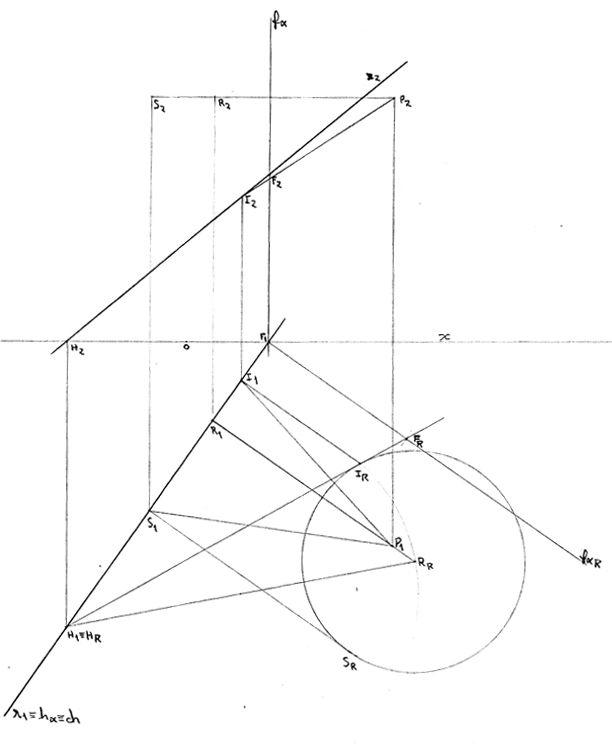
Exercício 38
Determina graficamente a verdadeira grandeza da distância entre os pontos R e S, situados no 1º diedro.
Dados
- o ponto R resulta da interseção de três planos - θ, α e β;
- o ponto S tem 9 cm de afastamento e abcissa igual à do ponto R;
- o plano θ é horizontal e tem 3 cm de cota;
- o plano α é de topo, interseta o eixo x num ponto com 3 cm de abcissa e faz um diedro de 45º (a.d.) com o plano horizontal de projeção;
- o plano β está definido pelo seu traço frontal e pelo ponto A (-6;-5; 5). O traço frontal interseta o eixo x num ponto com 1 cm de abcissa e faz com este eixo um ângulo de 45º (a.d.);
- os pontos R e S são simétricos em relação a um plano de rampa que forma um diedro de 45º com o plano horizontal de projeção.
Proposta de resolução
Exercício 39
Determina graficamente a verdadeira grandeza da distância do ponto P ao plano α.
Dados
- ambos os traços, nos planos de projeção, do plano α fazem ângulos de 80º (a.d.) com o eixo x;
- o plano α interseta o eixo x num ponto com abcissa nula;
- P (4; 7; 9)
Proposta de resolução
Exercício 40
Determina as projeções do ponto P, sabendo que a distância deste ponto aos pontos A, B e C é a mesma.
Dados
- A (5; 0; 0); B (0; -1; 6); C (-2; 6; 1);
- o ponto P tem cota nula.
Proposta de resolução
Problemas métricos - Ângulos (41-42)
Exercício 41
Determina, em dupla projeção ortogonal, as projeções da reta r, sabendo que esta faz um ângulo de 60º com o plano α.
Dados
- o plano α interseta o eixo x num ponto com 4 cm de abcissa e os seus traços fazem ângulos de 30º (a.d.) e de 45º (a.d.) com este eixo, respetivamente o traço e o traço horizontal;
- a reta r contém os pontos R (2; 6; 6) e S;
- o ponto S situa-se no 1º diedro, tem 2,5 de cota e pertence ao plano α.
Proposta de resolução
Exercício 42
Determina a verdadeira grandeza do ângulo entre uma reta vertical e o plano θ.
Dados
- o plano θ está definido pelos pontos A, B e C.
- A (2; 0; 0); B (2; 6; 2); C (-6; -2; -6)
Proposta de resolução
Secções (43-44)
Exercício 43
Representa as projeções do sólido resultante da secção produzida numa esfera por um plano projetante frontal. Considere o sólido mais próximo do plano horizontal e projeção.
Dados
- os pontos A (2; 4; 8), B (-1; 3; 5) e C (8; 4) pertencem à circunferência de interseção do plano secante com a superfície esférica;
- o centro da esfera tem 5 cm de cota.
Proposta de resolução
Exercício 44
Representa as projeções do sólido resultante da secção produzida num tetraedro pelo β13. Considera o sólido compreendido entre o plano secante e o plano horizontal de projeção.
Dados
- A (6; 4; 7) é um dos 4 vértices do tetraedro;
- uma das faces está contida no plano horizontal de projeção;
- a aresta de menor afastamento é fronto-horizontal.
Proposta de resolução
Sombras (45-46)
Exercício 45
Numa folha de formato A4 (ao alto), representa as projeções de um triângulo [RST].
Determina a sombra projetada, nos planos de projeção, pelo triângulo.
Utiliza a direção luminosa convencional.
Dados
- R (9; 2; 4); S (2; 14; 0); T (-3; 2; 10).
Proposta de resolução
Exercício 46
Representa as projeções de um cone oblíquo situado no 1º diedro, de acordo com os dados abaixo apresentados. Utilizando a direção luminosa convencional, determina a sombra própria do cone e a sua sombra real nos planos de projeção.
Dados
- a sombra do cone no plano horizontal de projeção é um círculo com 4 cm de raio e tem centro no ponto C (-4; -2; 0);
- a base do cone é tangente ao plano frontal de projeção e está contida num plano projetante frontal;
- uma, e só uma, geratriz do cone tem a direção da luz;
- o vértice do cone pertence ao eixo x e tem abcissa superior à do ponto C.
Proposta de resolução
Axonometrias ortogonais (47-50)
Exercício 47
Construa uma representação axonométrica ortogonal de uma forma tridimensional, composta por um paralelepípedo retângulo e por um prisma triangular reto. Todos os vértices têm coordenadas positivas.
Considera, no desenho final, apenas o traçado das arestas visíveis do sólido.
Sistema axonométrico
Dados
- cada sólido tem uma face contida no plano coordenado xy;
- as bases do prisma triangular são triângulos retângulos e estão contidas em planos de perfil;
- o paralelepípedo tem duas faces frontais;
- os pontos D (8; 4; 2) e E (0; 0; 2) são extremos de uma diagonal de uma das faces do paralelepípedo
- os pontos F (3; 4; 2) e G (0; 10; 0) são extremos de uma diagonal de uma das faces do prisma.
Proposta de resolução
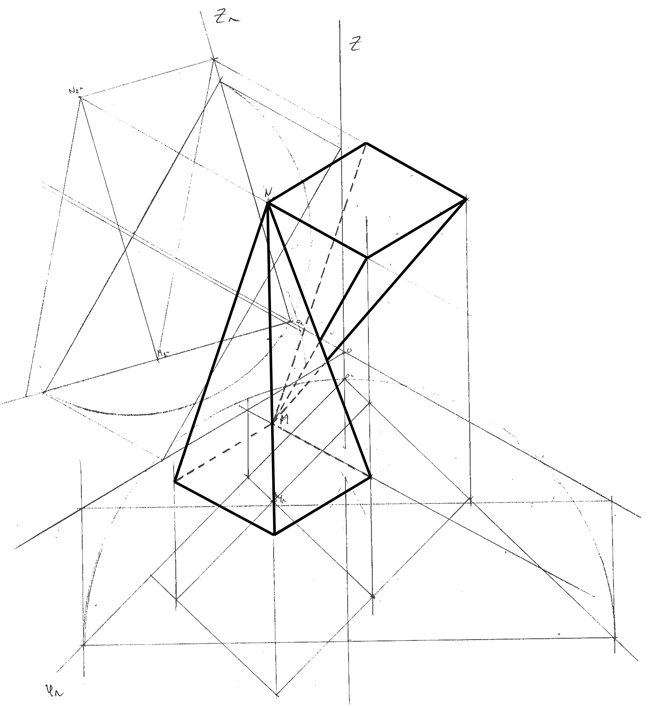
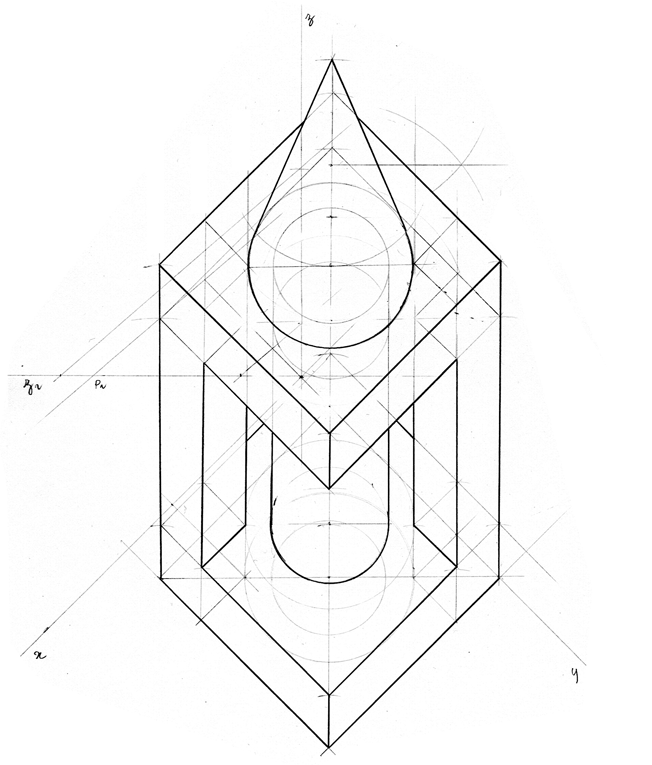
Exercício 48
Construa uma representação axonométrica ortogonal de uma forma tridimensional, composta por uma pirâmide triangular e por um prisma triangular regular. Todos os vértices têm coordenadas positivas.
Identifica, a traço interrompido, as arestas invisíveis do sólido.
Sistema axonométrico
Dados
- uma das bases do prisma está contida no plano coordenado xy;
- as faces laterais do prisma são quadrados;
- o segmento de reta [MN] é uma das arestas da base superior do prisma;
- M tem 6 cm de abcissa e pertence ao plano coordenado xz; N tem 4 cm de afastamento;
- a base da pirâmide coincide com a base superior do prisma;
- uma das faces laterais da pirâmide, [MNV], é equilátera e paralela ao plano axonométrico.
Proposta de resolução
Exercício 49
Constrói uma representação axonométrica ortogonal de uma forma tridimensional, composta por duas pirâmides quadrangulares oblíquas. O sólido fica situado no 1º triedro. Identifica, a traço interrompido, as arestas invisíveis do sólido.
Sistema axonométrico
Dados das pirâmides
- o segmento de reta [MN] é uma aresta lateral comum às duas pirâmides, M (4; 1; 0) e N (4; 1; 8);
- o ponto M é o vértice principal de uma das pirâmides e um dos vértices da base da outra pirâmide;
- a aresta lateral [MN] é perpendicular às bases das pirâmides;
- ambas as bases têm 4 cm de lado;
- cada pirâmide tem uma face lateral paralela ao plano xz;
- a aresta de menor abcissa é uma das arestas de maior cota, do sólido composto.
Proposta de resolução
Exercício 50
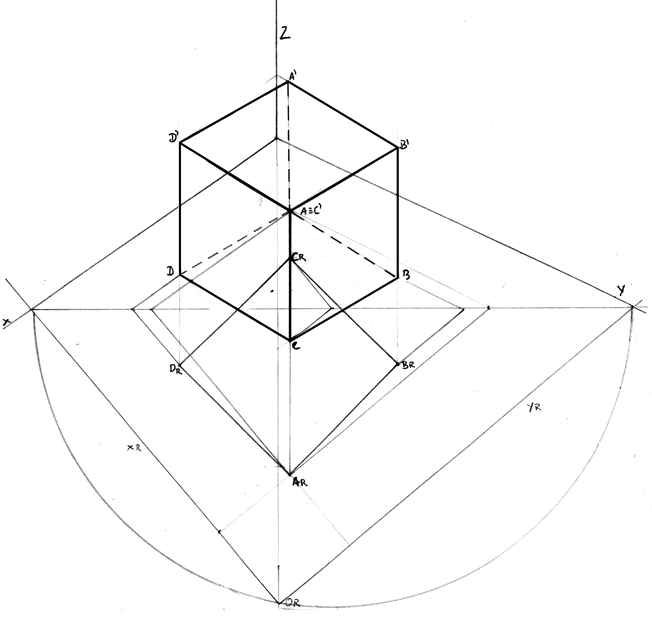
Construa uma representação axonométrica ortogonal de um prisma quadrangular regular. O sólido fica situado no 1º triedro. Identifica, a traço interrompido, as arestas invisíveis do sólido.
Sistema axonométrico
- anisometria - xÔz=125°; yÔz=115°.
Dados do prisma quadrangular regular:
- uma das bases está assente no plano xy;
- uma das diagonais internas (espaciais) é perpendicular ao plano axonométrico e contém o vértice A (3; 3; 0);
- as bases têm 5 cm de lado.
Proposta de resolução
Axonometrias oblíquas (51-53)
Exercício 51
Representa a projeção axonométrica oblíqua de uma forma tridimensional, composta por dois prismas quadrangulares.
Considere, no desenho final, apenas o traçado das arestas visíveis do sólido
Sistema axonométrico
- cavaleira;
- o eixo axonométrico x faz um ângulo de 155º com o eixo axonométrico z;
- Considera os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente de baixo para cima, e o eixo x, orientado positivamente da direita para a esquerda;
- as projetantes fazem ângulos de 55º com o plano axonométrico.
Dados
- um dos prismas é regular e tem uma face contida em cada um dos planos coordenados;
- R (3; 3; 7) é um vértice do prisma;
- o outro prisma é oblíquo e tem as bases de perfil (paralelas ao plano coordenado yz);
- o segmento de reta [RS] é uma das diagonais da base de menor abcissa;
- S (3; 0; 4);
- a diagonal interna (espacial) do prisma oblíquo que tem um dos extremos em R é projetante.
Proposta de resolução
Exercício 52
Constrói uma representação axonométrica oblíqua de uma forma tridimensional, composta por um prisma quadrangular oblíquo e por um prisma triangular regular.
Considera, no desenho final, apenas o traçado das arestas visíveis do sólido
Sistema axonométrico
- militar (planométrica);
- o eixo axonométrico x faz um ângulo de 125º com o eixo axonométrico z;
- Considera os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente de baixo para cima, e o eixo x, orientado positivamente da direita para a esquerda.
- as projetantes fazem ângulos de 50º com o plano axonométrico.
Dados
- os pontos R (0; 8; 4) e S (4; 8; 4) são extremos de uma aresta lateral do prisma triangular;
- este prisma tem uma face lateral contida no plano coordenado xy;
- as bases do prisma quadrangular têm 4 cm de lado e são horizontais;
- a aresta lateral de maior afastamento e de menor abcissa deste prisma pertence ao plano coordenado yz, faz um ângulo de 60º com o plano coordenado xy e o ponto R é o seu ponto médio;
- a aresta de menor afastamento do sólido composto é paralela ao eixo x e tem cota nula.
Proposta de resolução
Exercício 53
Constrói uma representação axonométrica oblíqua da forma tridimensional representada em tamanho natural, em tripla projeção ortogonal, apresentada na figura.
Sistema axonométrico
- militar (planométrica);
- o eixo axonométrico x faz um ângulo de 135º com o eixo axonométrico z;
- considera os eixos orientados em sentido direto: o eixo z, vertical, orientado positivamente de baixo para cima, e o eixo x, orientado positivamente da direita para a esquerda;
- as projetantes fazem ângulos de 50º com o plano axonométrico.
Dados
Proposta de resolução